In our previous lesson, we saw how the scientific evidence interrelates to choices atheists and believers must make about the creation. As stated, we assume that the student understands we are talking about the weight of the evidence, not absolute proof. We assumed that you accept the fact that there is reality and that you do exist. We then looked at the choices about that existence. The evidence supports the fact that there was a beginning. Scientific conservation laws demand that this beginning must have been caused. The diagram below gives a graphic representation of these choices.

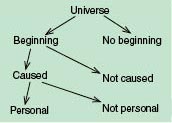The final question in this logical sequence is "What was the cause?" If the cause was a personal God, there are certain attributes that should appear in the creation. We should see order, design, intelligence, purpose, and planning all around us. In sharp contrast to this view, the atheist position maintains there is no such thing as a personal God who created the cosmos. If this is the case, then the universe is totally the product of chance. There is no design, no purpose, no intelligence, no planning--everything is the result of rote mechanistic, opportunistic chance. The quotations of Dawkins and Huxley in Lesson 1 express this viewpoint very well.

There is an amazing contrast between the position of the believer in God and the atheist on the question of origins as we will see in this lesson.

INTUITIVE DESIGN FEATURES IN THE COSMOS

There are a myriad of things that man can see all around him which show design and planning, but which we cannot analyze mathematically. The incredible migratory journeys of butterflies, birds, eels, whales, fish, and many other forms of life are accomplished by a bewildering array of devices and techniques. Migrations are beautifully designed not only in their accomplishment, but also in the ecological benefits they provide. Reproduction of all kinds demonstrates wisdom and planning.

A skeptic will react to this kind of example with the statement that we are using a "god of the gaps." When our knowledge improves, we will be able to explain these phenomena just as other mysteries of nature have been explained by scientists in the past. The complexity of the things we have referred to makes such a statement unlikely, but the point is well taken that “whiz bang’’ appeals have their limitations. For that reason, let us look at some statistical evidence which is of a different nature.

CAN A PLANETARY SYSTEM SUITABLE FOR LIFE OCCUR BY CHANCE?

Let us make the assumption that the cosmos began by a big bang--by chance alone. At this point we are not interested in what banged or who caused the bang--let us simply assume that it happened. Now let us ask this question: What are the mathematical probabilities that ANY KIND of life (not necessarily ours) could occur by chance alone from the big bang or expansion?

Notice that this is not an ad-hoc argument. We are not saying we are here--what are the odds of us being here? (This would be logically invalid.) We are saying let's go back before the big bang and ask, "What are the mathematical probabilities that any kind of life on any kind of functional planet could occur by chance alone?"

There are a myriad of factors that have to be "right" for any kind of life to exist. One of those factors is the kind of galaxy in which we are located. The galaxy in the picture to the right is the kind of galaxy in which we live. It is known as a spiral galaxy type b. What that means is that we have a certain shape, a great deal of interstellar material, stars of a certain age, and so forth. Interestingly enough, our galaxy is a very rare kind of galaxy in space. Eighty percent of all galaxies in space are of a different type, such as the galaxy in the picture to the left. This is an elliptical galaxy. There are 10 basic types of elliptical galaxies plus a variety of dwarf elliptical galaxies. These galaxies contain no interstellar material to speak of, so there is nothing from which to make terrestrial planets. How can we realistically talk about life existing in a galaxy where there are no planets?

The stars in elliptical galaxies are young and hot, totally unable to produce any kind of a life-supporting planet. In addition, there are barred-spiral galaxies, irregular galaxies, Seyfert galaxies, and various other types and subtypes--all of which have conditions that would destroy any kind of life. What are the mathematical probabilities of having the right kind of galaxy by chance alone? There are approximately 20 different kinds of galaxies, but only one type could reasonably be believed to contain any kind of life-supporting planet. The odds could conservatively be one out of 20--ignoring the relative number of each type of galaxy present.

Another factor that is critical to the existence of life is our location in the galaxy. A cross-section of our galaxy is shown below.

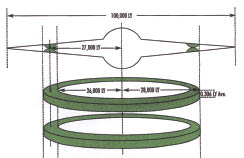Any solar system located along the equator of the galaxy would have a very low probability of long term survival. Not only is there a high concentration of matter along the equatorial axis, but the gravitational force of that matter is higher. Collisions are much more likely and gravitation, magnetic, and electrical forces that can disturb the stability of a solar system are also greater. The green area of the galaxy cross-section picture represents a "safe" area where a solar system could exist for a very long time in stability. This is called the Galactic Habitable Zone (GHZ) by astronomers. What are the mathematical odds of being in a GHZ? To determine this, we simply divide the volume of the shaded area by the volume of the whole galaxy. The safe "doughnut" above and below the equatorial plane has been estimated by some astronomers to have a one-in-a-million ratio to the volume of the whole galaxy, so the odds of being in the right place by chance could be a comparable figure.

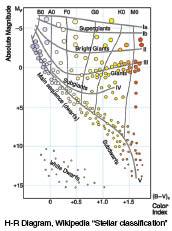The kind of star that we orbit also is critical to the survival of any kind of life in a solar system. Our sun is an unusually small, cool, stable star with just the right kind of electromagnetic emissions. Most stars in space are bigger, have a different temperature, give off the wrong kind of light (such as microwaves or X-rays), and/or are irregular in behavior. The Hertzsprung-Russell Diagram shown on the next page plots the luminosity of the star against the temperature of the star. Every star in space can be plotted on the diagram, but only a very small number have the right mass, size, age, kinds of radiation, and the like, to support any kind of life. There are massive numbers of different types of stars in space yet only a star like our sun can reasonably be believed to support any kind of life. What are the odds of getting the right kind of star by chance alone? You could conservatively estimate the odds to be one in a thousand.

The planet on which we live also offers conditions critical to our survival. Any kind of life will have to have the right kind of planet. The distance to the sun is critical to the existence of water and many other compounds needed for life. The size of the planet determines its atmospheric makeup. The rotation rate, the existence of a magnetic field, the structure of the atmosphere, and a myriad of other factors are all critical for the existence of any kind of life.

In addition to all of these factors, we have to consider the odds of being in the right place in space. If a black hole were located in the neighborhood of the earth or any other life-supporting planet, it would make life a total impossibility and would likely destroy both the planet and its sun.

Chemical problems also exist in the development of any kind of life. The existence of water is critical for life to exist. It seems there are literally hundreds of conditions that have to be “right” for any kind of life to exist anywhere.

When we look at odds such as one-in-a-million, or one-in-a-thousand, or even one-in-a-hundred, we can see that the probabilities are low. But there are billions of stars in space and there may be billions of planets as well. If there are enough places out there, it will happen! All we need are enough places and enough time and the situation will ultimately be right. We have already mentioned in our discussion that there are a very large number of stars in space. Our galaxy alone contains some 100 billion stars (10¹⁰). It has been estimated that there may be millions of galaxies (10⁶). Even if there were billions or hundreds of billions of galaxies, we are talking about something on the order of a maximum of 10²⁰ stars. Is this enough to allow any kind of life to come into existence by chance alone?

You might look at the probabilities that we have identified in our previous discussion which are summarized in the table below and say, "Yes, the odds of each of those events is way below a number like one in 10²⁰." That is certainly true, but there is another mathematical point that we have not yet discussed.

Let me illustrate by a very simple example. Suppose that I were to hold out a deck of well-shuffled playing cards to you and ask you to draw a single card blindfolded. What would be the mathematical odds of drawing the ace of spades? One in 52 is the correct answer. Now suppose that I told you to draw twice and to draw the ace of spades each time. What would be the odds of successfully doing that? If you are familiar with the mathematics of this situation, you know that the odds are 1 out of 52 times 1 out of 52.

1/52 x 1/52 = 1/2,704

When you have two events that must both be successful to obtain a desired result, you multiply the probabilities of each event. To draw the ace of spades out of a shuffled deck four times in a row back to back would be:

1/52 x 1/52 x 1/52 x 1/52 = 1/7,311,616

In other words, the total probability increases logarithmically as we increase the number of variables that have to be considered for a successful conclusion.

The application of this mathematical principle to the table should be obvious. It does no good to be in the right kind of galaxy if you are in the wrong place in that galaxy. It does no good to be in the right kind of galaxy and in the right place in that galaxy if you are going around the wrong kind of star or are too close or too far from that star. In other words, every one of the conditions in the table would have to be right. What you have to do then is to multiply the parameters listed in the table plus the hundreds that have not been included. Just using the numbers in the table (conservative and very incomplete though they are) we would get:

1/20 x 1/10,000 x 1/1,000 x 1/40 x 1/10 x 1/5 x 1/100 x 1/10 x 1/1,000 x 1/1,000 = 1/4 X 10²⁰ in round numbers.

All of this is to get A BALL OF ROCK IN THE RIGHT PLACE! Now we would have to multiply this number by the odds of life occurring by chance alone! Scientists and mathematicians like Murray Eden of MIT, Fred Hoyle of Cambridge, Francis Crick (co-discoverer of the structure of DNA), and others have shown that the odds of getting life by chance according to the models of Stanley Miller, Sidney Fox, and others are in the order of 10¹⁰⁰⁰! Their computations use the same concepts that we have developed in this lesson. Even a philosopher like Antony Flew, who was a champion of atheism, has admitted that life of any kind is not possible by chance alone. WE ARE NOT THE PRODUCT OF CHANCE!

SUMMARY

As we have seen, the atheistic faith that matter is eternal is impossible to believe from a scientific standpoint (Lesson 1). We have seen that it is illogical to believe that the beginning was uncaused because it forces us to accept the idea that matter can come from nothing, which invalidates all of science. We have seen that the caused beginning cannot logically or mathematically be a product of chance. It is statistically impossible to believe that the myriad of conditions necessary for any kind of life to occur could happened by chance. There is intelligence, purpose, design, order, and direction in the cosmos which speaks of a personal intelligence.

What must this personal intelligence be like? Are we talking about "the old engineer in the sky?" What properties are required of this intelligence and is there any religious belief system that is in accord with this concept? That is the subject of our next lesson.

Return to the Main Page for the Intermediate Correspondence Course.

12/15/2011